Question

Geometry Unit 7 Lesson 7. Please Help Picture attached.

Answer 1

The coordinates of orthocenter of the triangle are (1,5).

Explanation:

The given vertices are A(0,6), B(4,6) and C(1,3).

Orthocenter of a triangle is the intersection point of all altitudes.

The product of slopes of two perpendicular lines is -1.

The slope of AB is

`m_(AB)=(y_2-y_1)/(x_2-x_1)=(6-6)/(4-0)=0`

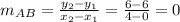
The slope of AB is 0, therefore slope of line which is perpendicular to AB is
`(-1)/(0)`.

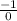Point slope form of a line is

`y-y_1=m(x-x_1)`

Where, m is the slope.

The equation of altitude on AB form C is

`y-3=(1)/(0)(x-1)`

`0=x-1`

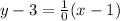
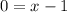
`x=1` ..... (1)

Slope of BC is

`m_(BC)=(y_2-y_1)/(x_2-x_1)=(6-3)/(1-4)=1`

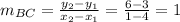
The slope of BC is 1 therefore the slope of altitude on BC from A is -1.

The equation of altitude on BC from A is

`y-6=-1(x-0)`

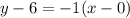
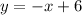`y=-x+6` ..... (2)

Using (1) and (2) we get

`x=1, y=5`

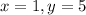
The intersection point of two altitudes is (1,5). Therefore coordinates of orthocenter of the triangle are (1,5).