Question

Calculate the sum of the first 36 terms of the arithmetic sequence defined in which a36=14 and the common difference is d=1/8

Answer 1

ANSWER


`S_ {36} = 425.25`


EXPLANATION

Since we know the 36th term to be 14, we can find the first term using the formula,


`u_n= a+(n-1)d`



This implies that,



`14= a+(36-1) * (1)/(8)`





`14 = a + (35)/(8)`


`a = 14 - (35)/(8)`




`a =9.625`


We can now find the sum of the first 36 terms using the formula,


`S_n= (n)/(2) (2a + (n - 1)d)`


`S_ {36} = (36)/(2) (2 * 9.625+ (36 - 1) * (1)/(8) )`



`S_ {36}= 18(2 * 9.625+ (35) * (1)/(8) )`




`S_ {36}= 18(23.625 ) = 425.25`

Answer 2

425.25

Explanation:

Since we are given 36th term as 14 and we know common difference is
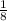`(1)/(8)`, it means that from the first term, we add
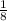`(1)/(8)` to each and get 14 on the 36th term. To figure out the first term, thus, we have to subtract
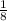`(1)/(8)` 35 times from 14. Let's do it to get first term:

`14-35((1)/(8))=(77)/(8)=9.625`

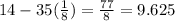
The sum of arithmetic sequence formula is:

`S_(n)=(n)/(2)[2a+(n-1)d]`

Where,

• 
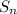  `S_(n)` is the sum of nth term (we want to figure this out for first 36 terms)
• 
  `a` is the first term (we figured this out to be 9.625)
• 
  `n` is the term number (36 for our case)
• 
  `d` is the common difference (given as
  `(1)/(8)`)

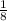Substituting all the values, we get:

`S_(36)=(36)/(2)[2(9.625)+(36-1)((1)/(8))]\\S_(36)=18[19.25+4.375]\\S_(36)=18[23.625]\\S_(36)=425.25`

First answer choice is right.