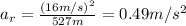Question

A stopwatch starts while race car travels at 4 m/s from the pit area and accelerates at a uniform rate to a speed of 23 m/s in 2 s moving on a circular track of radius 527 m.

Assuming constant tangential acceleration, find

(a) the tangential acceleration, and

(b) the radial acceleration,at the instant when the speed is v = 16

Once you have both of those ... find the magnitude of a at any moment

Answer 1

(a) Tangential acceleration:
`9.5 m/s^2`

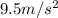
The tangential acceleration is given by:

`a_t = (v-u)/(t)`

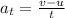
where

v = 23 m/s is the final velocity of the car

u = 4 m/s is the initial velocity of the car

t = 2 s is the time taken for the car to accelerate from u to v

Substituting the numbers into the formula, we find

`a_t = (23 m/s-4 m/s)/(2 s)=9.5 m/s^2`

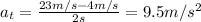
(b) Radial acceleration:
`0.49 m/s^2`

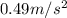
The radial acceleration is equivalent to the centripetal acceleration, which is given by:

`a_r = (v^2)/(r)`

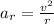
where

v = 16 m/s is the tangential speed

r = 527 m is the radius of the circular orbit

Substituting numbers, we find

`a_r = ((16 m/s)^2)/(527 m)=0.49 m/s^2`