
Other method:

zeros of numerator and denominator are x = -2 and x = 4.
Look at the second picture.
for x < -2 → x + 2 < 0 and x - 4 < 0
therefore
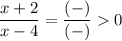
for -2 < x < 4 → x + 2 > 0 and x - 4 < 0
therefore
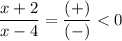
for x > 4 → x + 2 > 0 and x - 4 > 0
therefore
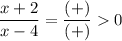
Answer: B) -2 < x < 4