Question

In the diagram, VZ/YZ=WZ/XZ. To prove that △VWZ ~ △YXZ by the SAS similarity theorem, which other sides or angles should be used?

Answer 1

∠VZW ≅ ∠YZX

Explanation:

I got it right on edg.

Answer 2

The angles
`\angle VZW\cong \angle YZX` are used to prove the similarity of triangles VWZ and YXZ.

Explanation:

Given information:
`(VZ)/(YZ)=(WZ)/(XZ)`

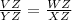
Two triangles are called congruent if their corresponding sides are in same proportion or the corresponding angles are same.

If two corresponding sides of triangle have same proportion and their inclined angle is same, then by SAS rule of similarity both triangles are similar.

From the given figure it is noticed that the ∠VZW and ∠YZX are vertically opposite angles. The vertically opposite angles are always equal.

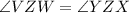`\angle VZW=\angle YZX` (Vertically opposite angles)

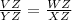`(VZ)/(YZ)=(WZ)/(XZ)` (Given)

By SAS rule of similarity

`VWZ\sim YXZ`

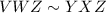
Therefore the angles
`\angle VZW\cong \angle YZX` are used to prove the similarity of triangles VWZ and YXZ.