Answer:
Mathew will take 5 seconds to ride down the hill.
Explanation:
Given equation is:
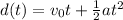
Matthew is cycling of a speed of 4 meters/second. So,

When he starts down a hill, the bike accelerates at a rate of 0.4 m/s². So,
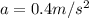
The vertical distance from the top of the hill to the bottom of the hill is 25 meters. So,
 meters.
meters.
Plugging the values into the above equation, we will get......
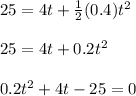
Using quadratic formula, we will get.......

(Negative value is ignored as the time can't be negative)
So, Mathew will take 5 seconds to ride down the hill.