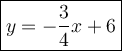Slope intercept form of a line that has a slope of -3/4 and passes through (4, 3)

Question

asked Nov 11, 2022 55.8k views

1 Answer

Ravi Gadag · Answer 1 · 2022-11-14T18:11:50+0000

We have the given slope value and the coordinate point that the graph passes through.

y = mx + b

where m = slope and b = y-intercept. Substitute the value of slope in the equation.

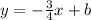
y = - (3)/(4) x + b

We have the given coordinate point as well. After we substitute the slope, we substitute the coordinate point value in the equation.

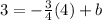
$3 = - (3)/(4) (4) + b \\$

Solve the equation for b-term

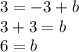
$3 = - 3 + b \\ 3 + 3 = b \\ 6 = b$

The value of b is 6. We substitute the value of b in the equation.

y = - (3)/(4) x + 6

We can also use the Point-Slope form to solve the question.

y - y_1 = m(x - x_1)

Given the y1 and x1 = the coordinate point value.

Substitute the slope and coordinate point value in the point slope form.

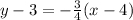
y - 3 = - (3)/(4) (x - 4)

Simplify/Convert into Slope-intercept

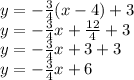
$y = - (3)/(4) (x - 4) + 3 \\ y = - (3)/(4) x + (12)/(4) + 3 \\ y = - (3)/(4) x + 3 + 3 \\y = - (3)/(4) x + 6$

$\large \boxed {y = - (3)/(4) x + 6}$