Answer:
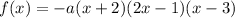 where a>0.
where a>0.
To graph the the polynomial, begin in the left top of quadrant 2. Then draw downwards to the first real zero on the x-axis at -2. Cross the x-axis and then curve back up to 1/2 on the x-axis. Cross through again and curve back down to cross for the last time at 3 on the x-axis. The graph then ends going down towards the right in quadrant 4. It forms an s shape.
Explanation:
The real zeros are the result of setting each factor of the polynomial to zero. By reversing this process, we find:
- zero 1/2 is factor (2x-1)
We write them together with an unknown leading coefficient a which is negative so -a.
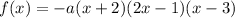 where a>0
where a>0
The leading coefficient of a polynomial determines the direction of the graph's end behavior.
- A positive leading coefficient has the end behavior point up when an even degree and point opposite directions when an odd degree with the left down and the right up.
- A negative leading coefficient has the end behavior point down when an even degree and point opposite directions when an odd degree with the left up and the right down.
- This graph has all odd multiplicity. The graph will cross through the x-axis each time at its real zeros.
To graph the the polynomial, begin in the left top of quadrant 2. Then draw downwards to the first real zero on the x-axis at -2. Cross the x-axis and then curve back up to 1/2 on the x-axis. Cross through again and curve back down to cross for the last time at 3 on the x-axis. The graph then ends going down towards the right in quadrant 4. It forms an s shape.