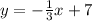Question

What is the equation of the line, in slope-intercept form, that passes through the point (0,7) and is perpendicular to the line y=3x−5?

Answer 1

=12

Explanation:

7=3(0)-5

7=-5

7+5

=12

Im pretty sure this is the answer

Answer 2

`y=-(1)/(3)x+7`

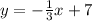
Explanation:

The slope-intercept form is:
`y=mx+b`; where m is the slope, and b is the y-axis interception.

So, the problem is asking for a line that it's perpendicular to
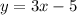`y=3x-5`. This perpendicular relation means that the line we have to find have an inverse and opposite slope than the given line, that's expressed like this:

`m_(1)m_(2)=-1`

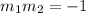
That expression is the condition to have perpendicular lines. So, the given line has a slope of 3, now we can find the slope of the new line:

`m_(1)m_(2)=-1\\m_(1)=(-1)/(m_(2))=-(1)/(3)`

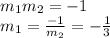
Now we have the slope of the new perpendicular line, we use the point-slope formula to find its equation:

`y-y_(1)=m(x-x_(1))\\ y-7=-(1)/(3)(x-0)\\y=-(1)/(3)x+7`

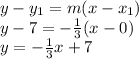
Therefore, the slope-intercept form of the new perpendicular line is:

`y=-(1)/(3)x+7`