Question

HELPP!! can someone please help me with my math? (The page) thanks!!

Answer 1

Question 1 part B (You've got A) Ben's rate of change (Slope) Is 0.15 Shown as the variable m in the equation y=0.15x+49

Question 2 part A Angela's initial value is 60 (Y-intercept) shown on the graph at the point (0,60)

Question 2 part B Ben's initial value is 49 (Y-intercept) shown as the variable b in the equation y=0.15x+49

Question 3 part A Angela's price for talking 200 minutes would be 80$ as shown on the graph as the point (200, 80) (the answer is the y value)

Question 3 part B Ben's price if he talked for 200 minutes would be 79 if you substituted 200 for the x value, multiplied it by 0.15 then added 49, you'd get 30+49 to give you 79$ as your final cost.

Explanation:

Answer 2

A. The rate of change for the two points are:

Angela: $0.1 per minute.

Ben: $0.15 per minute.

B. The initial values for the two points are;

Angela: $60.

Ben: $49.

C. The total cost of each plan are as follows;

Angela: $80 per minute.

Ben: $79 per minute.

The slope-intercept form of the equation of a straight line is given by this mathematical equation;

y = mx + c

Where:

• m represents the slope or rate of change.
• x and y are the points.
• c represents the y-intercept or initial value.

Part A.

The rate of change for the two points are as follows;

Rate of change =
`(y_2-y_1)/(x_2-x_1)`

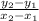
Rate of change (Angela) = (72 - 60)/(120 - 0)

Rate of change (Angela) = $0.1 per minute.

Based on the equation y = 0.15x + 49 in slope-intercept form, we have;

Ben: $0.15 per minute.

Part B.

The initial values represents the y-intercept and they are as follows;

Angela: $60.

Ben: $49.

Part C.

When x is 200 minutes, the total cost of each plan are as follows;

Angela: y = 0.10x + 60

y = 0.10(200) + 60

y = $80 per minute.

Ben: y = 0.15x + 49

y = 0.15(200) + 49

y = $79 per minute.