First, recall that
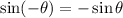
So if
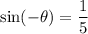 , then
, then
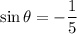 .
.
Second,
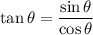
We know that
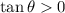 and
and
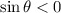 , which means we should also have
, which means we should also have
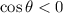 .
.
Third,
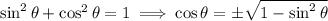
but as we've already shown, we need to have
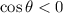 , so we pick the negative root.
, so we pick the negative root.
Finally,
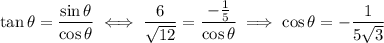
Unfortunately, none of the given answers match, so perhaps I've misunderstood one of the given conditions... In any case, this answer should tell you everything you need to know to find the right solution from the given options.