Answer:
f(x) opens downward and has a maximum value.
Explanation:
The given function is
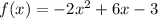
It is a quadratic function and hence represents a parabola.
The standard form of a quadratic equation/parabola is
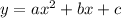
- If a>0, then the parabola opens upward and vertex is the minimum point
- If a<0, then the parabola opens downward and vertex is the maximum point
Comparing the given equation with the standard form of parabola, we get
a = -2, b = 6, c = -3
Since, a = -2 <0. Hence, the parabola opens downward and has a maximum value.