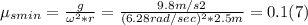Question

what equastion do you use to solve Riders in a carnival ride stand with their backs against the wall of a circular room of diameter 5.0 m. The room is spinning horizontally about an axis through its center at a rate of 60 rev/min when the floor drops so that it no longer provides any support for the riders. What is the minimum coefficient of static friction between the wall and the rider required so that the rider does not slide down the wall?

Answer 1

μsmín = 0.1

Step-by-step explanation:

• There are three external forces acting on the riders, two in the vertical direction that oppose each other, the force due to gravity (which we call weight) and the friction force.
• This friction force has a maximum value, that can be written as follows:

`F_(frmax) = \mu_(s) *F_(n) (1)`

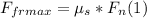
where μs is the coefficient of static friction, and Fn is the normal force,

perpendicular to the wall and aiming to the center of rotation.

• This force is the only force acting in the horizontal direction, but, at the same time, is the force that keeps the riders rotating, which is the centripetal force.
• This force has the following general expression:

`F_(c) = m* \omega^(2) * r (2)`

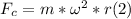
where ω is the angular velocity of the riders, and r the distance to the

center of rotation (the radius of the circle), and m the mass of the

riders.

Since Fc is actually Fn, we can replace the right side of (2) in (1), as

follows:

`F_(frmax) = m* \mu_(s) * \omega^(2) * r (3)`

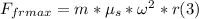
• When the riders are on the verge of sliding down, this force must be equal to the weight Fg, so we can write the following equation:

`m* g = m* \mu_(smin) * \omega^(2) * r (4)`

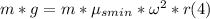
• (The coefficient of static friction is the minimum possible, due to any value less than it would cause the riders to slide down)

• Cancelling the masses on both sides of (4), we get:

`g = \mu_(smin) * \omega^(2) * r (5)`

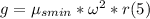
• Prior to solve (5) we need to convert ω from rev/min to rad/sec, as follows:

`60 rev/min * (2*\pi rad)/(1 rev) *(1min)/(60 sec) =6.28 rad/sec (6)`

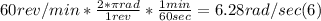
• Replacing by the givens in (5), we can solve for μsmín, as follows:

`\mu_(smin) = (g)/(\omega^(2) *r) = (9.8m/s2)/((6.28rad/sec)^(2) *2.5 m) =0.1 (7)`