Question

Which graph represents the function f(x) = (3/2)^-x Image for option 1Image for option 2Image for option 3Image for option 4

Answer 1

65

Explanation:

Answer 2

An exponential decay function
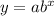`y =ab^x` where a is the initial value and 0<b<1.

Given the function:
`f(x) = ((3)/(2))^(-x)`

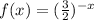
or we can write this as;

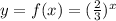`y=f(x) = ((2)/(3))^(x)` ......[1]

The domain for this function is all real number and the range is, y>0.

also this function is decreasing because b =
`(2)/(3)` < 1.

First find the y-intercept:

y-intercepts defined as the graph crosses the y-axis

substitute x =0 in [1] to find x;

`y = ((2)/(3))^(0) = 1`

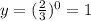
y-intercepts: (0, 1).

End behavior of the given function:

• as we increase x, f(x) values grows smaller and approaching to zero i.e,

as
`x \rightarrow \infty` ,
`f(x) \rightarrow 0`

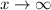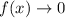
• as we decreases s, f(x) grows without bound. i.e,

as
`x \rightarrow -\infty` ,
`f(x) \rightarrow \infty`

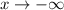As you can see the graph of this function below in the attachment.