Answer:
The answer is below
Explanation:
For a normal distributed population with a mean (μ), and a standard deviation (σ), if a sample size of n is selected from the population, the mean of the sample (
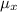 ) = μ and the standard deviation of the sample (
) = μ and the standard deviation of the sample (
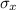 ) =
) =

Let the normal distribution population have a standard deviation of σ. If the standard deviation is to be decreased by half, the sample size (n) needed is:
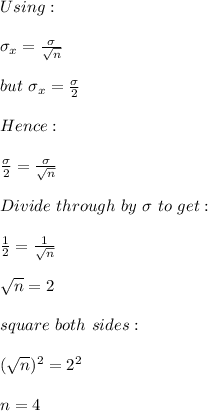
To decrease the standard deviation of the sampling distribution by half we need a sample size of 4