Question

Chapman’s brickyard sells bricks and blocks. A brick costs $0.38 and a block costs $1.56. The brickyard filled a $24.80 order, which contained 28 items

a. Write a system of equations that can be used to find the number of bricks and blocks in the order.
b. How many blocks were in the order?

Answer 1

a)
`\left \{ {{0.38x+1.56y=24.80} \atop {x+y=28}} \right.`

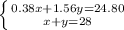
b) 12 blocks and 16 bricks.

Explanation:

Let x represent the number of bricks and y represent the number of blocks. Each brick costs $0.38; this gives us the expression 0.38x. Each block costs $1.56; this gives us the expression 1.56y. Together they totaled $24.80; this gives us the equation

0.38x + 1.56y = 24.80

We also know that the number of bricks, x, added to the number of blocks, y, totaled 28; this gives us

x + y = 28

To solve this, we will use substitution. First we will isolate x in the second equation by subtracting y from each side:

x + y = 28

x + y - y = 28 - y

x = 28 - y

Now we substitute this in place of x in the first equation:

0.38(28 - y) + 1.56y = 24.80

Using the distributive property, we have

0.38(28) - 0.38(y) + 1.56y = 24.80

10.64 - 0.38y + 1.56y = 24.80

Combining like terms gives us

10.64 + 1.18y = 24.80

Subtract 10.64 from each side:

10.64 + 1.18y - 10.64 = 24.80 - 10.64

1.18y = 14.16

Divide both sides by 1.18:

1.18y/1.18 = 14.16/1.18

y = 12

There were 12 blocks sold.

Substituting this into the second equation gives us

x + 12 = 28

Subtract 12 from each side:

x + 12 - 12 = 28 - 12

x = 16

There were 16 bricks sold.