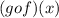Answer:
The statement that is true about functions is:
If f and g are function then,
B. (f+g)(x)=f(x)+g(x)
Explanation:
A)
Let us define f(x)=x² and g(x)=1
then we have:
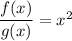
and
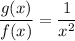
Hence, we get:
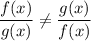
Hence, option: A is incorrect.
B)
Option: B is always true.
(f+g)(x)=f(x)+g(x)
C)
Let us define f(x)=x²
Then
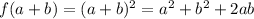
and
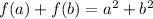
Hence, we get:
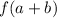 is not always equal to
is not always equal to
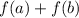
D)
Let us suppose
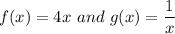
Now,
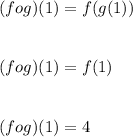
and
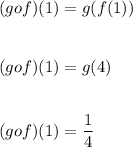
Hence, we get:
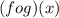 is not always equal to
is not always equal to