Answer:
the length of the simple pendulum is 0.25 m.
Step-by-step explanation:
Given;
mass of the air-track glider, m = 0.25 kg
spring constant, k = 9.75 N/m
let the length of the simple pendulum = L
let the frequency of the air-track glider which is equal to frequency of simple pendulum = F
The oscillation frequency of air-track glider is calculated as;
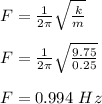
The frequency of the simple pendulum is given as;
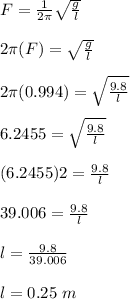
Thus, the length of the simple pendulum is 0.25 m.