Question

What must be the length of a simple pendulum if its oscillation frequency is to be equal to that of an air-track glider of mass 0.250 kg attached to a spring of force constant 9.75 N/m

Answer 1

To determine the length of a simple pendulum with the same frequency as an air-track glider attached to a spring, equate the formula for the mass-spring system frequency with the simple pendulum frequency formula, and solve for the length.

Step-by-step explanation:

To find the length of the simple pendulum that has the same oscillation frequency as an air-track glider attached to a spring, we use the formula for the frequency of a mass-spring system and set it equal to the formula for the frequency of a simple pendulum. The frequency of a mass-spring system is given by f = √(k/m)/(2π) where k is the spring constant and m is the mass, and the frequency of a simple pendulum is given by f = (1/2π) √(g/L), where g is the acceleration due to gravity and L is the length of the pendulum.

By setting these two frequencies equal and solving for L, we can determine the required length of the pendulum. For a spring with a constant k of 9.75 N/m and a mass of 0.250 kg, the equation becomes √(9.75/0.250)/(2π) = (1/2π) √(9.81/L). Solving this equation gives us the length L needed for the pendulum to have the same frequency as the mass-spring system.

Answer 2

the length of the simple pendulum is 0.25 m.

Step-by-step explanation:

Given;

mass of the air-track glider, m = 0.25 kg

spring constant, k = 9.75 N/m

let the length of the simple pendulum = L

let the frequency of the air-track glider which is equal to frequency of simple pendulum = F

The oscillation frequency of air-track glider is calculated as;

`F = (1)/(2\pi ) \sqrt{(k)/(m) } \\\\F = (1)/(2\pi ) \sqrt{(9.75)/(0.25) } \\\\F = 0.994 \ Hz`

The frequency of the simple pendulum is given as;

`F = (1)/(2\pi) \sqrt{(g)/(l) } \\\\2\pi(F) = \sqrt{(g)/(l) } \\\\2\pi (0.994) = \sqrt{(9.8)/(l) } \\\\6.2455 = \sqrt{(9.8)/(l) } \\\\(6.2455)2 = (9.8)/(l) \\\\39.006 = (9.8)/(l) \\\\l = (9.8)/(39.006) \\\\l = 0.25 \ m`

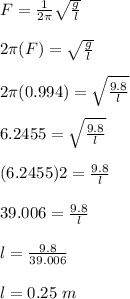
Thus, the length of the simple pendulum is 0.25 m.