Question

One root of f(x)=x3-4x2-20x+48 is x=6. What are all the factors of the function? Use the remainder theorem.

Answer 1

(x - 6)(x + 4)(x - 2)

Explanation:

since x = 6 is a root then (x - 6) is a factor

x³ - 4x² - 20x + 48 ÷ (x - 6)

= (x - 6)(x² + 2x - 8)

= (x - 6)(x + 4)(x - 2) ← factors of f(x)

Answer 2

The other two factors are (x-2) and (x+4)

Explanation:

Given one root of polynomial
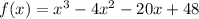`f(x)=x^3-4x^2-20x+48` which is x=6

we have to find the other factors of given function.

Polynomial:
`f(x)=x^3-4x^2-20x+48`

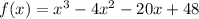
If x=6 is one of the root then by remainder theorem

Put x=6

`f(6)=0`

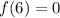
Hence, by synthetic division the quotient is

`x^2+2x-8`

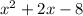
By middle-term splitting method

`x^2+4x-2x-8`

`x(x+4)-2(x+4)`

`(x-2)(x+4)`

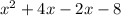
The other two factors are (x-2) and (x+4)