Question

The mass of a deuterium nucleus 21H is less than its components masses. Calculate the mass defect.________ amu

Answer 1

0.002389

Step-by-step explanation:

Use the equation the other person used to answer but with the numbers that are given on this assignment!

Answer 2

The mass defect of a deuterium nucleus is 0.001848 amu.

Step-by-step explanation:

The deuterium is:

`^(A)_(Z)X \rightarrow ^(2)_(1)H`

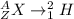
The mass defect can be calculated by using the following equation:

`\Delta m = [Zm_(p) + (A - Z)m_(n)] - m_(a)`

Where:

Z: is the number of protons = 1

A: is the mass number = 2

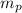`m_(p)`: is the proton's mass = 1.00728 amu

`m_(n)`: is the neutron's mass = 1.00867 amu

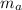`m_(a)`: is the mass of deuterium = 2.01410178 amu

Then, the mass defect is:

`\Delta m = [1.00728 amu + (2- 1)1.00867 amu] - 2.01410178 amu = 0.001848 amu`

Therefore, the mass defect of a deuterium nucleus is 0.001848 amu.

I hope it helps you!