Question

Dana has 800 yards of fencing to enclose a rectangular area. Find the dimensions of the rectangle that maximize the enclosed area. What is the maximum? area

Answer 1

Perimeter of rectangle states that total distance around the outside, which can be found by adding together the length of each side.

As per the given statement, Dana has 800 yards of fencing to enclose a rectangular area.

Therefore, perimeter of rectangle = 800 yards.

Perimeter(P) of rectangle is given by :

P = 2(x+y) where x is the length and y is the width of the rectangles respectively.

Then,

2(x+y) = 800

Divide both sides by 2 we get;

x+y =400

or

y = 400 -x .....[1]

We know, the area(A) of rectangle is given by

A = xy .....[2]

Substitute equation [1] into [2] we get;l

A = x(400-x)

using distributive property
`a\cdot (b+c) = a\cdot b+ a\cdot c`

`A = 400x -x^2`

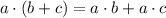
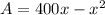
or

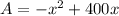`A =-x^2+400x` ......[3]

To maximize the enclosed area.

For a quadratic function in standard form
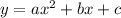`y =ax^2+bx+c` , the axis of symmetry is a vertical line given by;

`x = -(b)/(2a)`

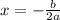
Then; we have from equation [3]

a = -1 and b = 400

By axis of symmetry;

`x = -(b)/(2a)` =
`-(400)/(2 \cdot -1) =(400)/(2) = 200`

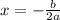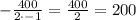
Substitute in equation [1] to solve for y:

y = 400 - 200 = 200

The dimensions of the rectangle that maximize enclosed area are:

x = 200 units and y = 200 units.

Maximum area =
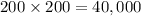`200 * 200 = 40,000` square units.

We can say that maximum area of rectangle will always be a square