Answer:
Two real solutions
Explanation:
Given is a graph of a parabola with quadratic equation.
We know that
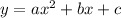
has solution as x intercepts of the graph.
Using the above we find that the given graph has solution at the x intercepts.
X intercepts are 0 and -4
Hence the solutions are two real and they are x=0 and x =-4
Verify:
The graph is the transformation of
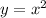 by verical shift of 4 units down and horizontal shift of 2 units left
by verical shift of 4 units down and horizontal shift of 2 units left
So equation would be
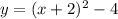
Simplify to get
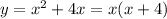
Hence solutoins are x=0 or x = -4