Here are the prices of five new skateboards, in dollars

Question

asked Sep 1, 2019 172k views

2 Answers

Teadotjay · Answer 1 · 2019-09-05T17:36:53+0000

Answer: Option (A) The new standard deviation is greater than $27.

Step-by-step explanation:

If a sixth skateboard having price of $450 is added to the sample, the new sample set will be the following:

75, 82, 100, 120, 140, 450.

Let us first find the mean of the above sample set.

Mean =
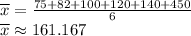
$\overline{x}=(75+82+100+120+140+450)/(6)\\ \overline{x} \approx 161.167$

Now that we have mean, let's find the variance.

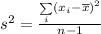
$s^2 = \frac{\underset{i} \sum (x_i - \overline x)^2}{n-1}$

Where n is the number of samples in the set (which in this case is 6).

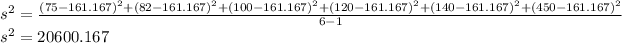
$s^2 = ((75-161.167)^2+(82-161.167)^2+(100-161.167)^2+(120-161.167)^2+(140-161.167)^2+(450-161.167)^2)/(6-1) \\s^2 = 20600.167$

Now that we have variance, it's time to find the new standard deviation by taking the square-root of the variance, as follows:

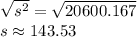
$√(s^2) = √(20600.167) \\s \approx 143.53$

$143.53 > $27

New standard deviation is greater than the old standard deviation.

Therefore, the correct answer is Option (A) The new standard deviation is greater than $27.