Question

Which of these choices show a pair of equivalent expression? Check all that apply.

Answer 1

C and D

Explanation:

using the rules of exponents

A

`125^(3/7)` =
`\sqrt[7]{125^3}` ≠
`\sqrt[3]{125^7}`

B

(
`√(12)`)^7 =
`12^(7/2)` ≠
`12^(1/7)`

C

(
`√(4)`)^5 =
`4^(5/2)` ← correct

D

(
`√(8)`)^9 =
`8^(9/2)` ← correct

Answer 2

Answer: The correct options are

(C)
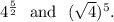
`4^(5)/(2)~~\textup{and}~~(√(4))^5.`

(D)
`8^(9)/(2)~~\textup{and}~~(√(8))^9.`

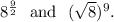
Step-by-step explanation: We are to select the correct pairs that shows equivalent expressions.

We will be using the following property of exponents and radicals :

`(\sqrt[b]{x})^a=x^(a)/(b).`

Option (A) :

The given expressions are

`(\sqrt[3]{125})^7~~\textup{and}~~125^(3)/(7).`

We have

`(\sqrt[3]{125})^7=125^(7)/(3)\\eq 125^(3)/(7).`

So, the expressions are not equivalent and option (A) is incorrect.

Option (B) :

The given expressions are

`12^(1)/(7)~~\textup{and}~~(√(12))^7.`

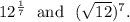
We have

`12^(1)/(7)=\sqrt[7]{12},\\\\(√(12))^7=12^(7)/(2).`

So,

`12^(1)/(7)\\eq (√(12))^7.`

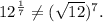
Therefore, the expressions are not equivalent and option (B) is incorrect.

Option (C) :

The given expressions are

`4^(5)/(2)~~\textup{and}~~(√(4))^5.`

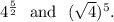
We have

`(√(4))^5=4^(5)/(2)`

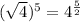
Therefore, the expressions are equivalent and option (C) is correct.

Option (D) :

The given expressions are

`8^(9)/(2)~~\textup{and}~~(√(8))^9.`

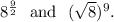
We have

`(√(8))^9=8^(9)/(2)`

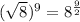
Therefore, the expressions are equivalent and option (D) is correct.

Thus, (C) and (D) are the correct options.