Answer: The correct options are
(C)
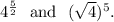
(D)
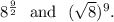
Step-by-step explanation: We are to select the correct pairs that shows equivalent expressions.
We will be using the following property of exponents and radicals :
![(\sqrt[b]{x})^a=x^(a)/(b).](https://img.qammunity.org/2019/formulas/mathematics/college/s7zy46jv1ss47k4t5vslst7lgluirkhp7q.png)
Option (A) :
The given expressions are
![(\sqrt[3]{125})^7~~\textup{and}~~125^(3)/(7).](https://img.qammunity.org/2019/formulas/mathematics/college/rdjxnry21wsyu25dd2szceip2d5p9pwvfs.png)
We have
![(\sqrt[3]{125})^7=125^(7)/(3)\\eq 125^(3)/(7).](https://img.qammunity.org/2019/formulas/mathematics/college/4820q87dvkkqux0wnmqgag3928ht39kgkc.png)
So, the expressions are not equivalent and option (A) is incorrect.
Option (B) :
The given expressions are
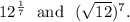
We have
![12^(1)/(7)=\sqrt[7]{12},\\\\(√(12))^7=12^(7)/(2).](https://img.qammunity.org/2019/formulas/mathematics/college/hyyepj8n0n3d7sqjchpi0htkg3ytg1i8z4.png)
So,
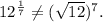
Therefore, the expressions are not equivalent and option (B) is incorrect.
Option (C) :
The given expressions are
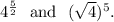
We have
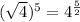
Therefore, the expressions are equivalent and option (C) is correct.
Option (D) :
The given expressions are
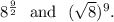
We have
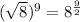
Therefore, the expressions are equivalent and option (D) is correct.
Thus, (C) and (D) are the correct options.