Answer:

Explanation:
If points M and N are the midpoints of sides AC and BC of △ABC, then segment MN is a midline segment of the triangle ABC. By the triangle midline theorem, MN║AB and is half of AB.
Since
- angle C is common;
- MN║AB, then angles A and M are congruent and angles B and N are congruent,
then triangles ABC and MNC are similar by AAA theorem with
 factor of similarity. Thus,
factor of similarity. Thus,
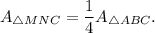
The area of the quadrilateral ABNM is

Then
