Question

Plzz someone help!!! i will mark barinliest!!!worth 20 points!

3. The sequence 6, 18, 54, 162, … shows the number of pushups Kendall did each week, starting with her first week of exercising.

(a) What is common ratio in this sequence?

(b) How many pushups will Kendall do on the 20th week?


step-by-step!

Answer 1

a: 3

b: 183514968.4

Explanation:

find the geometric sequence and plug it in

Answer 2

Given:

The sequence 6, 18, 54, 162, …

To Find:

• The common ratio in this sequence
• and the number of pushups Kendall will do on the 20th week.

Answer:

Kendall will do 6973568802 pushups in the 20th week.

Explanation:

The given sequence 6, 18, 54, 162, ... is a geometric series.

A geometric series is a sequence of numbers where each succeeding term can be found by multiplying the previous term with a constant factor which is called the common ratio.

We see that in the given sequence, each successive term can be found by multiplying the previous term by 3.

18 = 6 multiplied by 3

54 = 18 multiplied by 3

162 = 54 multiplied by 3

and so on.

So, the common ratio is 3.

The general form of a geometric series can be written as

`a, ar, ar^(2), ar^(3), ar^(4), ...`

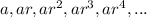
where a denotes the intial term and r denotes the common ratio.

The nth term of the series can be found by the formula

`a_(n)=ar^(n-1)`

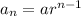
For the given sequence, intial term a = 6 and common ratio r = 3.

To find the number of pushups Kendall will do on the 20th week, we need to calculate the 20th term.

That is,

`a_(20)=ar^(20-1)=(6)(3^(19))\\\\=(6)(1162261467)=6973568802`

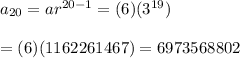
Thus, Kendall will do 6973568802 pushups in the 20th week.