Answer:
x -intercepts (nearest to hundredths) = 82.75
y -intercepts (nearest to hundredths) = -2.15
Explanation:
Given the function: y= log (12x+7) - 3 ......[1]
x-intercepts states that the graph crosses the x-axis or
In other words x-intercepts is the point on the graph where y= 0.
Now, substitute the values of y = 0 in [1] to solve for x;
0 = log(12x + 7) - 3
Add both sides 3 we get;
0 + 3 = log(12x + 7) - 3+ 3
Simplify:
3 = log (12x+7)
Using :
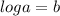 ⇒
⇒
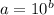
Then;
12x + 7 =

or
12x + 7 = 1000
Subtract 7 to both sides of an equation we have;
12x + 7 - 7= 1000 - 7
Simplify:
12x = 993
Divide both sides by 12 we get;
x = 82.75
Therefore, x - intercept = 82.75
Y-intercepts states that the graph crosses the y-axis or
In other words y-intercepts is the point on the graph where x= 0
Substitute the value of x =0 in [1] to solve for y;
y = log(12(0) +7) -3
y = log(7) -3
y = 0.84509804- 3 = - 2.15490196
therefore, y -intercepts (nearest to hundredths) is, -2.15