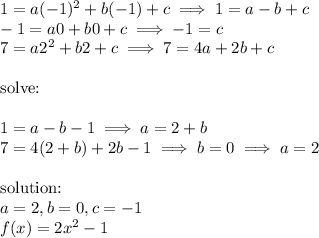Answer:
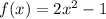
Explanation:
To determine a quadratic function fully, three known points are needed. Each point can be used to determine one parameter of the function. A general quadratic is as follows:
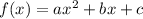
where a,b, and c are to be determined.
Use the individual points from the table to set up an equation system with the unknowns a,b, and c, then solve: