Question

What are the roots of `2x + 6 = -(5)/(x)`?

A. `(3stackrel(+)(-) i)/(2)`
B. `(-3stackrel(+)(-) i)/(2)`
C. `(-3stackrel(+)(-) 2i)/(4)`
D. `(3stackrel(+)(-) isqrt(2))/(4)`

Answer 1

B.
`x = (-3 \pm i)/(2)`

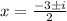
Explanation:

2x + 6 = -5/x Multiply both sides by x

2x² + 6x = -5 Add 5 to each side

2x² + 6x + 5 = 0

==============

Apply the quadratic formula

`x = (-b\pm√(b^2-4ac))/(2a)`

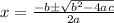
a = 2; b = 6; y = 5

`x = (-6\pm√(6^2-4* 2 * 5))/(2* 2)`

`x = (-6\pm√(36-40))/(4)`

`x = (-6\pm√(-4))/(4)`

`x = (-6\pm2i)/(4)`

`x = -(3)/(2)\pm(i)/(2)`

`x = (-3 \pm i)/(2)`

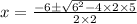
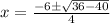
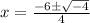
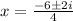
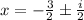
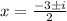
The graph of the parabola never reaches the x-axis, so there are no real roots.