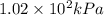Question

Type the correct answer in the box. Express your answer to three significant figures. A balloon is filled with 0.250 mole of air at 35°C. If the volume of the balloon is 6.23 liters, what is the absolute pressure of the air in the balloon? The absolute pressure of the air in the balloon is kilopascals.

Answer 1

Answer : The absolute pressure of the air in the balloon is
`1.02* 10^2kPa`

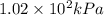
Explanation :

Using ideal gas equation :

`PV=nRT`

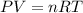
where,

P = Pressure of the air in the balloon = ?

V = Volume of the balloon = 6.23 L

n = number of moles of air filled in balloon = 0.250 mole

R = Gas constant =
`0.0821L.atm/mol.K`

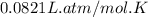
T = Temperature of the balloon =
`35^oC=273+35=308K`

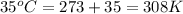
Putting values in above equation, we get:

`P* 6.23L=0.250mole* (0.0821L.atm/mol.K)* 308K`

`P=1.01atm`

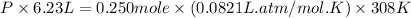
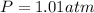
Now we have to convert the pressure of the air from 'atm' to 'kilopascals'.

Conversion used :

1 atm = 101.325 kPa

So, 1.01 atm = 1.01 × 101.325 = 102.34 kPa ≈
`1.02* 10^2kPa`

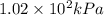
Therefore, the absolute pressure of the air in the balloon is
`1.02* 10^2kPa`

Answer 2

∴ The absolute pressure of the air in the balloon in kPa = 102.69 kPa.

Step-by-step explanation:

• We can solve this problem using the general gas law:

PV = nRT, where,

P is the pressure of the gas (atm),

V is the volume of the gas in L (V of air = 6.23 L),

n is the no. of moles of gas (n of air = 0.25 mole),

R is the general gas constant (R = 0.082 L.atm/mol.K),

T is the temperature of gas in K (T = 35 °C + 273 = 308 K).

∴ P = nRT / V = (0.25 mole)(0.082 L.atm/mol.K)(308 K) / (6.23 L) = 1.0135 atm.

• Now, we should convert the pressure from (atm) to (kPa).

1.0 atm → 101.325 kPa,

1.0135 atm → ??? kPa.

∴ The absolute pressure of the air in the balloon in kPa = (101.325 kPa)(1.0135 atm) / (1.0 atm) = 102.69 kPa.