Question

1. How does orbital velocity relate to altitude above the surface of a planet?

2. How is orbital velocity different from tangential (linear) velocity?

Answer 1

1.

Orbital velocity is the velocity of a satellite with which it goes around a planet in a stable orbit.

We know that orbital velocity is given bu:

`v_o=\sqrt{(GM)/(r)}`

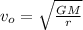
Where, G is the gravitational constant, M is the mass of the planet and r is the distance from the planet.

The orbital velocity is inversely proportional to the distance from the planet i.e. the altitude. Hence, As the altitude above the surface of a planet increases, the orbital velocity decreases.

2.

The tangential velocity is constant as it is tangential to the circular (orbital) path. Orbital velocity is the velocity of a satellite with which it goes around a planet in a stable orbit. Orbital velocity keeps on changing as the direction changes in the circular path. Orbital velocity can be written as the sum of tangential velocity and radial velocity.