Question

Solve for x.

logx+log3=log18

Enter your answer in the box.

x =

Answer 1

x = 6.00001

Explanation:

We are given the following log problem to solve for x:

log(x) + log(3) = log(18)

log(x) + 0.477121 = 1.255273

Adding -0.477121 to both the sides to get:

log(x) + 0.477121 + (−0.477121) = 1.255273 + (−0.477121)

log(x) + 0 = 0.778152

Dividing both the sides by 1 to get:

log(x) + 0/1 = 0.778152/1

log(x) = 0.778152

Solving the logarithm to get:

log(x) = 0.778152

10log(x) = 100.778152

x = 6.00001

Answer 2

x=6

Explanation:

We are given the equation here:

`logx+log3=log18`

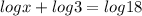
Now we have log on both sides and we have to solve for x here.

At first let us bring log3 to the right side.

Here log3 is in addition on the right, so we will apply opposite operation of addition on the left. Opposite operation of addition is subtraction.

So subtracting log3 from right side, we have,

`logx=log18-log3`

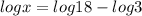
Now we use division property of log,

`loga-logb=log(a)/(b)`

`logx=log(18)/(3)`

`logx=log6`

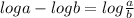
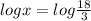
Now comparing both sides ,

x=6