Question

A boat is pulled into a dock by a rope with one end attached to the front of the boat and the other end passing through a ring attached to the dock at a point 5 feet higher than the front of the boat. The rope is being pulled through the ring at the rate of 0.6 ft/sec. How fast is the boat approaching the dock when 13 feet of rope are out

Answer 1

The boat is approaching the dock at 0.65 ft/sec when 13 feet of rope are out.

Explanation:

Let x be the length of rope and y be the distance between boat and dock.

Height of point where a ring attached =z=5 feet

`(dx)/(dt)=-0.6ft/sec`

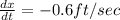
x=13 feet

Using Pythagoras theorem

`H^2=P^2+B^2`

`x^2=z^2+y^2`

`x^2=5^2+y^2=25+y^2`

`(13)^2=25+y^2`

`169-25=y^2`

`144=y^2`

`y=12 feet`

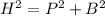
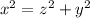
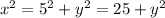
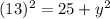
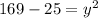
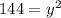
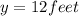
Differentiate w.r.t t

`2x(dx)/(dt)=2y(dy)/(dt)`

`x(dx)/(dt)=y(dy)/(dt)`

`13(-0.6)=12(dy)/(dt)`

`(7.8)/(12)=(dy)/(dt)`

`(dy)/(dt)=-0.65feet/sec`

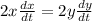
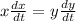
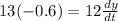
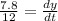
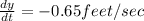
Hence,the boat is approaching the dock at 0.65 ft/sec when 13 feet of rope are out.