Question

A young couple purchases their first new home in 2002 for $120,000. They sell it to move into bigger home in 2007 for $150,000. First, we will develop an exponential model for the value of the home. The model will have the form V(t)=V0ekt. Let t be years since 2002 and V(t) be the value of the home.

Answer 1

`V(t)=120000*e^((0.044)t)`

Explanation:

If the given equation is
`V(t)=V₀*e^(kt)` .............(i)

Here from the question it is given that

V(t) = $150,000

V₀=$120,000

t= 2007-2002=5 years

e≅2.718

k=?

Now for the Value of k putting all values in equation (i)

`150000=120000*e^(k(5))`

`e^(5(k))=(150000)/(120000)`

`e^(5(k))=(5)/(4)`

Now taking Natural log on both sides of the equation

㏑ (e^{5(k)})= ㏑\frac{5}{4}

as we Know that ln(e)=1

so

5k = 0.223

dividing both sides by 5 gives

k =
`(0.223)/(5)`

k= 0.044

Now as we got the value of k we can form a general exponential equation which will be

`V(t)=V₀*e^((0.044)t)`

here value of v₀ is 120000

so equation will be

`V(t)=120000*e^((0.044)t)`

Answer 2

The exponential model for the value of the home is
`V(t)=120000e^(0.045t)`.

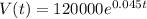Explanation:

According to the give information 2002 is the initial year and the value of the hom in 2002 is $120,000.

The model will have the form

`V(t)=V_0e^(kt)`

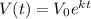
Where V₀ is initial value of home, k is a constant and t is number f years after 2002.

`V(t)=120000e^(kt)`

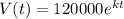
The value of home in 2007 is $150,000. Difference between 2007 and 2002 is 5 years. Therefore the value of function is 150000 at t=5.

`150000=120000e^(k(5))`

`(150000)/(120000)=e^(5k)`

`(5)/(4)=e^(5k)`

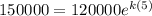
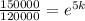
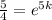
Take ln both sides.

`ln((5)/(4))=lne^(5k)`

`ln((5)/(4))=5k` (
`lne^a=a`)

`(ln((5)/(4)))/(5)=k`

`k=0.04462871\approx 0.045`

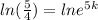
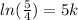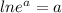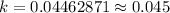
Therefore exponential model for the value of the home is
`V(t)=120000e^(0.045t)`.

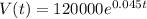Where t is number of years after 2002.