Mass of the object is given as
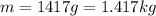
now the speed of object is given as
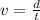
here we know that
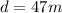
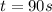
now we will have
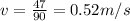
now we will have kinetic energy of the object as
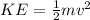
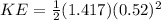
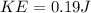
now the power is defined as rate of energy
so here we can find power as
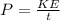
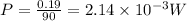
so above is the power used for the object