Answer:
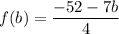
Explanation:
The given equation is

where, b is the input value and a is the output value of function f.
We need to find the formula for f(b) in terms of b.
It means we have to separate
 on one side because
on one side because
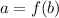 .
.
Consider the given equation.

Subtract 7b from both sides.
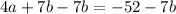
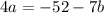
Divide both sides by 4.
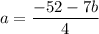
Substitute a=f(b).
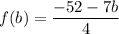
Therefore, the required formula is
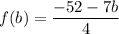 .
.