Answer:
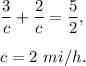
Explanation:
Let c miles per hour be the rate of the river current. If the rate at which the boat travels in still water is 5 times the rate of the river current, then the rate of the boat is 5c miles per hour.
1. Upstream the rate of the boat is 5c-c=4c miles per hour. To overcome 12 miles upstream it is needed

2. Downstream the rate of the boat is 5c+c=6c miles per hour. To overcome 12 miles downstream it is needed
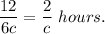
2. The total time is
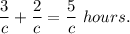
If the excursion boat on the river takes 2½ hours to make the trip to a point 12 miles upstream and to return, then
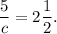
Solve this equation:
