Question

What eqwation of a parabola with a focus(6,-2) and a directrix x=-2

Answer 1

The equation of the parabola

( y +2 )² = 16 (x-2)

Explanation:

Step(i):-

Given the focus of the Parabola ( 6, -2 )

we know that the Focus of the Parabola

( h + a , k ) = ( 6 , -2 )

Comparing

h + a = 6 ...(i)

and k = -2

Given directrix of the parabola

x = -2

The directrix of the parabola x = h - a = -2

h - a = -2 ...(ii)

Adding (i) and (ii) equations , we get

h + a + h-a = 6 -2

2 h = 4

⇒ h = 2

Substitute 'h' = 2 in equation (i) , we get

h + a = 6

2 + a = 6

a = 6 -2 =4

Step(ii):-

The equation of the parabola having Vertex ( h,k) = (2 , -2) and a = 4

`(y-k)^(2) = 4a ( x-h)`

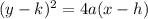
( y - (-2))² = 4 (4) ( x -2)

Final answer:-

The equation of the parabola

`(y-(-2))^(2) = 4(4) ( x-2)`

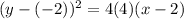
( y +2 )² = 16 (x-2)