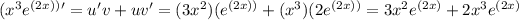Question

Derivative of

`x^(3)`
`e^(2x)`

Answer 1

`f(x)=x^3e^(2x)\\\\f'(x)=(x^3e^(2x))'\qquad\text{use}\ (f\cdot g)'(x)=f'(x)g(x)+f(x)g'(x)\\\\=(x^3)'(e^(2x))+(x^3)(e^(2x))'\\\\\text{use}\ (x^n)'=nx^(n-1)\ \text{and}\ (e^x)'=e^x\ \text{and}\ f'[g(x)]=f'(g(x))\cdot g'(x)\\\\=3x^2e^(2x)+x^3e^(2x)\cdot2\\\\=\boxed{3x^2e^(2x)+2x^3e^(2x)}`

Answer 2

The derivative of
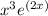`x^3e^{(2x)` can be found using the product rule of differentiation.

Step-by-step explanation:

The derivative of
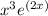`x^3e^{(2x)` can be found using the product rule of differentiation. The product rule states that the derivative of the product of two functions, u and v, is given by the formula (u*v)' = u'v + uv'.

Let
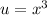`u = x^3` and
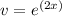`v = e^{(2x)`. Taking the derivatives of u and v, we have:

`u' = 3x^2v' = 2e^{(2x)`

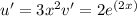
Using the product rule, the derivative of x^3e^{(2x) is:

`(x^3e^((2x)))' = u'v + uv' = (3x^2)(e^((2x))) + (x^3)(2e^((2x))) = 3x^2e^((2x)) + 2x^3e^((2x))`