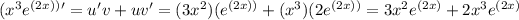The derivative of
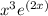 can be found using the product rule of differentiation.
can be found using the product rule of differentiation.
Step-by-step explanation:
The derivative of
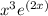 can be found using the product rule of differentiation. The product rule states that the derivative of the product of two functions, u and v, is given by the formula (u*v)' = u'v + uv'.
can be found using the product rule of differentiation. The product rule states that the derivative of the product of two functions, u and v, is given by the formula (u*v)' = u'v + uv'.
Let
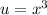 and
and
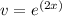 . Taking the derivatives of u and v, we have:
. Taking the derivatives of u and v, we have:

Using the product rule, the derivative of x^3e^{(2x) is: