ANSWER
The explicit formula that defines the sequence is
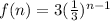
EXPLANATION
The given sequence is

The first term of this sequence is
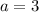
We can find the common ratio by expressing a subsequent term over a previous term and simplifying it.
The common ratio is
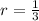
The formula for finding the nth term of the given geometric sequence is given by,
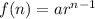
We now substitute the value of the first term and the common ratio in to the above formula to obtain,
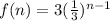
The correct answer is option D.