Question

What are the endpoint coordinates for the midsegment of △BCD that is parallel to BC¯¯¯¯¯?

Enter your answer, as a decimal or whole number, in the boxes.


(-2,-1) and (1,0)
Everyone have a blessed day, hope this helps :)

Answer 1

Explanation:

Answer 2

The endpoint coordinates for the mid segment of △BCD that is parallel to BC are (-2,-1) and (1,0).

Explanation:

The mid segment of a triangle a line segment that connecting the midpoint of two sides and parallel to the third side.

It is given that mid segment is parallel to BC, it means it is connecting the midpoints of BD and CD.

The midpoint formula,

`Midpoint=((x_1+x_2)/(2),(y_1+y_2)/(2))`

`\text{Midpoint of BD}=((-3-1)/(2),(1-3)/(2))=(-2,-1)`

`\text{Midpoint of CD}=((3-1)/(2),(3-3)/(2))=(1,0)`

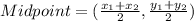
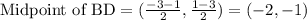
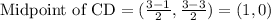
Therefore the endpoint coordinates for the mid segment of △BCD that is parallel to BC are (-2,-1) and (1,0).