Answer:
option-B
Explanation:
We are given
At the start of the year, 15 chameleons were introduced into a zoo
so,
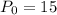
The population of chameleons is expected to grow at a rate of 41.42% every year
so, r=0.4142
and x represents the number of years since the chameleons were introduced into the zoo
now, we can set equation to find total population
and we get

now, we can plug values
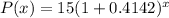

Average rate of change between 2 years and 4 years:
we can use formula
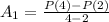
now, we can plug values
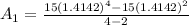
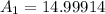
Average rate of change between 4 years and 6 years:
we can use formula

now, we can plug values
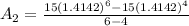

Average rate of change between 6 years and 8 years:
we can use formula
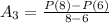
now, we can plug values
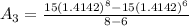
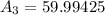
now, we will check each options
option-A:
we can see that
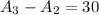
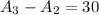
So, this is FALSE
option-B:
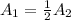
So, this is TRUE
option-C:
This is FALSE
option-D:
we got
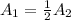
so, this is FALSE