Answer:
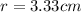
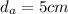
Explanation:
Let's use the radius equation to a circle inscribed into a triangle.
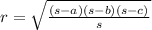
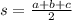
In our case a = 13 mc, b = 13 cm and c = 10 cm
Then, s will be s = 18 cm
Then the radius will be:
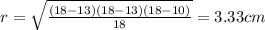
Now, the distance from the vertex to the nearest touchpont is given by:
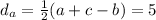
This value is the same for each side.
I hope it helps you!