Question

A triangle has two 13-cm sides and a 10-cm side. The largest circle that fits inside this triangle meets each side at a point of tangency. These points of tangency divide the sides of the triangle into segments of what lengths? What is the radius of the circle?

Answer 1

`r=3.33 cm`

`d_(a)=5 cm`

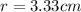
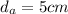
Explanation:

Let's use the radius equation to a circle inscribed into a triangle.

`r=\sqrt{((s-a)(s-b)(s-c))/(s)}`

`s=(a+b+c)/(2)`

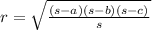
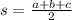
In our case a = 13 mc, b = 13 cm and c = 10 cm

Then, s will be s = 18 cm

Then the radius will be:

`r=\sqrt{((18-13)(18-13)(18-10))/(18)}=3.33 cm`

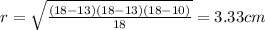
Now, the distance from the vertex to the nearest touchpont is given by:

`d_(a)=(1)/(2)(a+c-b)=5`

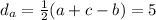
This value is the same for each side.

I hope it helps you!