Answer:
The determinant of the given matrix is:
a) -42
Explanation:
We are given a matrix let A as:
![A=\left[\begin{array}{ccc}5&4\\8&-2\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/5r13ryvuqy61gk9shiby3ty5w75nexdxi4.png)
Determinant of a matrix--
The determinant of a 2×2 i.e. a square matrix of order 2 is calculated as follows:
If:
![A=\left[\begin{array}{ccc}a&b\\c&d\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/zbywi1b4r9c8byi685q2voiwcw34dfd0m8.png)
then the determinant denoted by det(A) or |A| is given by:
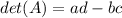
Here a=5, b=4 , c=8 and d= -2
Hence, the determinant is given by:
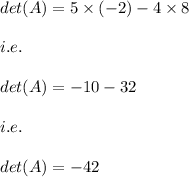
The correct answer is: Option: a)