Question

Find the determinant of the given matrix.

(5 4)
(8 - 2)=

a) -42

b) -22

c) 22

d) 42

Answer 1

Answer: -42

Step-by-step explanation: 2*2 matrices are easy to find the determinant with. Its just ad-bc, so (5*-2)-(4*8), which is -42

Answer 2

The determinant of the given matrix is:

a) -42

Explanation:

We are given a matrix let A as:

`A=\left[\begin{array}{ccc}5&4\\8&-2\end{array}\right]`

Determinant of a matrix--

The determinant of a 2×2 i.e. a square matrix of order 2 is calculated as follows:

If:

`A=\left[\begin{array}{ccc}a&b\\c&d\end{array}\right]`

then the determinant denoted by det(A) or |A| is given by:

`det(A)=ad-bc`

Here a=5, b=4 , c=8 and d= -2

Hence, the determinant is given by:

`det(A)=5* (-2)-4* 8\\\\i.e.\\\\det(A)=-10-32\\\\i.e.\\\\det(A)=-42`

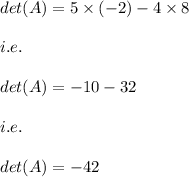
The correct answer is: Option: a)