Question

The graph shows the function ​ g(x) ​ . Select from the drop-down menu to correctly compare the growth factors for the exponential functions​​ ​ g(x) ​ and f(x)=5(3)^x .

The growth factor of​ f(x) is ___ the growth factor of ​ g(x) ​.

A: Greater Than
B: Less Than
C: Equal To

Answer 1

Less than

Explanation:

the other person is correct! I got it right on my homework

Answer 2

The correct option is B. The growth factor of​ f(x) is less than the growth factor of ​g(x).

Explanation:

In an exponential function

`y=C(1+r)^x`

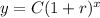
Where (1+r) is growth factor and r is the growth rate.

The given function is

`f(x)=5(3)^x`

Therefore growth factor of f(x) is 3.

From the graph it is noticed that it is an exponential function which is passing through (0,1) and (1,5).

Let the equation of g(x) is

`g(x)=ab^x`

`1=ab^0`

`1=a`

`g(x)=(1)b^x`

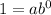
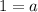
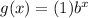
The graph passing through (1,5). so we get

`5=b^1`

`b=5`

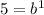
Therefore the value of a is 1 and value of b is 5.

The equation of g(x) is

`g(x)=1(5)^x`

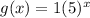
Therefore growth factor of g(x) is 5.

Since 3<5, therefore we can say that the growth factor of​ f(x) is less than the growth factor of ​g(x). Option B is correct.